Внутримолекулярное движение в двухатомной молекуле во время свободного пробега

• Во время свободного пробега двухатомной молекулы её атомы совершают плоское движение, которое либо приводит к диссоциации молекулы, либо представляет собой свободные двумерные колебания, в процессе которых циклически меняются с одной и той же частотой расстояние между ядрами атомов и угловая скорость вращательного движения.

   Потенциал взаимодействия

    Рассматриваются двухатомные молекулы, состоящие из одинаковых атомов. Сила взаимодействия между атомами в таких молекулах обусловлена ковалентной связью, работающей только на расстояниях d ≤ d_i, соответствующих перекрытию электронных облаков атомов. Если атомы расходятся на расстояние d > d_i, то происходит диссоциация (распад) молекулы.
Величина силы ковалентного взаимодействия F= F(d) зависит только от расстояния d между ядрами атомов и определяется потенциалом взаимодействия U(d) с помощью формулы
F(d) = – U ‘(d),
где символ «’» означает производную по переменной d.
Точный вид потенциала взаимодействия для атомов конкретного элемента определяется структурой их электронной оболочки и может быть определён только при решении соответствующей задачи для уравнения Шрёдингера, однако качественный характер зависимости одинаков для всех веществ.
Функция U(d) определена для всех d из интервала 0 < d ≤ d_i с точностью до постоянного слагаемого. Для целей данного раздела удобно выбрать величину этой константы таким образом, чтобы потенциал U(d) принимал всюду положительные значения, за исключением точки минимума d = d₀, где он обращается в нуль, а вторая производная достигает максимума (Рис. 1). При d < d₀  F(d) > 0 (атомы отталкиваются друг от друга), а при d > d₀  F(d) < 0 (атомы притягиваются друг к другу).

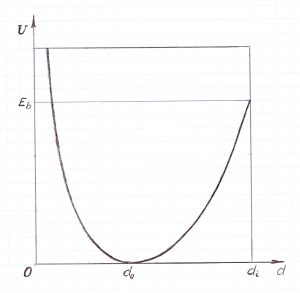
Рис.1. Потенциал взаимодействия U(d)

    Значение потенциала на правой границе интервала определения
U(d_i) = E_b
имеет физический смысл энергии связи между атомами, а при приближении к левому концу интервала функция U(d) неограниченно растёт:
U(d) → ∞.
      d → 0
Вторая производная потенциала взаимодействия U »(d) положительна на всём интервале определения, а третья производная U »'(d) отрицательна при d₀ ^≤ d ≤ d_i.

    Внутримолекулярное движение во время свободного пробега

       При описании движения атомов внутри молекулы их ядра трактуются как материальные точки с заданной массой т. Если использовать систему отсчёта, связанную с центром масс молекулы, то в период времени, когда рассматриваемая молекула удалена от других молекул газа на расстояние, большее d_i, можно считать, что её атомы образуют замкнутую систему. Из замкнутости системы следует наличие интегралов движения – полной энергии I (сумма кинетических энергий атомов и потенциальной энергии взаимодействия между ними), равного нулю вектора суммарного импульса атомов и вектора суммарного момента импульса М.
Задача определения законов движения ядер атомов при свободном пробеге молекулы является  частным случаем классической задачи двух тел, имеющей аналитическое решение. В выбранной системе отсчёта траектории атомов расположены в плоскости, проходящей через начало отсчёта и ортогональной вектору М. При этом в каждый момент времени положение атомов симметрично относительно начала отсчёта, а  вектора скоростей параллельны и противоположно направлены.
Введём в плоскости движения атомов полярные координаты (r, φ) с центром О, совпадающим с центром масс молекулы. Если ядро одного из атомов имеет в этой системе координаты (r, φ), то ядро второго – координаты (r, φ + π), а расстояние между ядрами d = 2r.

    Суммарная кинетическая энергия атомов К представляется в виде
К = m (r`<sup>2</sup> + r <sup>2</sup> φ`²) = ¼ m (d`<sup>2</sup> + d <sup>2</sup> φ`²),
где символ «`» означает производную по времени t.
Выбирая в качестве обобщённых координат системы переменные d и φ, мы получаем для функции Лагранжа L выражение:
L = ¼ m (d`² + d ² φ`<sup>2</sup>) – U(d),
откуда следуют дифференциальные уравнения движения:
         ½ m d«= ½ m d φ`² + F(d),                                                                          (1)
         ½ m (d ² φ`)`= 0.                                                                                           (2)
Уравнения (1), (2) полностью определяют закон движения, т.е. функции d(t) и φ(t), если в какой-либо момент времени t = t₀ заданы начальные условия – значения обобщенных координат и их производных по времени:
d(t₀) = d₀,       φ(t₀) = φ₀,
d`(t<sub>0</sub>) = d`₀,     φ`(t<sub>0</sub>) = φ`_0.
    Интегрирование равенства (2) по времени от t₀ до t даёт:
½ m d ² φ`= М,                                                                                             (3)
где М – постоянная величина, выражающаяся через начальные значения функций d и φ`:
М = ½ m d₀ ² φ`<sub>0</sub>.
Как нетрудно убедиться, модуль константы М совпадает с модулем вектора суммарного момента импульса.
Выражая φ` из (3)
φ`= 2 М m^–1 d ^–2                                                                                                (4)
и подставляя (4) в (1), имеем:
    ½ m d«= F_c (d) + F(d),                                                                                     (5)
где
F_c (d) = 2 М ² m^–1 d^–3 – центробежная сила.

     Равновесное расстояние между ядрами атомов

    Дифференциальное уравнение (5) определяет движение атомов вдоль оси, соединяющей их ядра (осевое движение). Точкой равновесия при осевом движении является зависящее от момента импульса М равновесное расстояние d_eq(М) между ядрами атомов, для которого центробежная сила, отдаляющая атомы друг от друга, уравновешивается силой притяжения атомов:
       F_c (d_eq) + F(d_eq) = 0.                                                                                         (6)
Очевидно, с ростом момента импульса величина d_eq(М) монотонно возрастает от d₀ при М = 0 до максимально возможной величины d_i при достижении моментом импульса критического значения
       М_С = [ ½ m U ‘(d_i) d_i³]^½,
при котором абсолютная величина силы притяжения равна U ‘(d_i).
В случае
       М > М_С                                                                                                           (7)
силы притяжения между атомами не могут противодействовать центробежным силам и молекула диссоциирует.

• Абсолютная величина момента импульса М может принимать значения в интервале от нуля до критического значения М_С, при котором происходит диссоциация молекулы.
• При изменении момента импульса от нуля до М_С равновесное расстояние между атомами возрастает от d₀ до d_i. 

    При достаточно малых значениях М отклонение равновесного расстояния от точки минимума d₀ потенциала относительно мало, так что выполняется условие
ζ = (d_eq – d₀) d₀^–1 << 1.
В линейном приближении по ζ имеем:
    F_c (d_eq) = F_c (d₀) (1 + ζ)^–3 ≈ F_c (d₀) (1 – 3ζ),                                                       (8)
    F(d_eq) = – U ‘(d_eq) = – U »(d₀) d₀ ζ.                                                                    (9)
Из (6) и (8), (9) следует, что при малых М величина ζ определяется формулой                                                                                                                                                                          ζ = μ₀ (3μ₀ + α₀) ^–1,                                                                                           (10)
где                                                                                                                                                                                                                                                                                                                    α₀ = ½  U »(d₀) d₀²,                                                                                                                                                                                                                                                                  μ₀ = М ² m^–1 d₀^–2.
Слова «достаточно малые значения М» в дальнейшем означают, что безразмерное отношение                                                                                                                                    ε = μ₀/α₀
мало по сравнению с единицей:                                                                                                                                                                                                                                                            ε << 1.                                                                                                            (11)
Как следует из (10), при выполнении условия (11) с точностью до малых порядка О(ε²)                                                                                                                                                        ζ ≈ ε,
                     d_eq ≈ d₀ (1 + ε).                                                                                             (12)

   Энергия внутреннего движения и её составляющие

    Умножение обеих частей равенства (5) на ½ d` и интегрирование результата по времени от t<sub>0</sub> до t приводит к формуле для интеграла I энергии внутреннего движения двухатомной молекулы:
I = Е<sub>аx</sub> + Е<sub>rot</sub>(d) + U(d),                                                                                     (13)
где
Е<sub>аx</sub> = ¼ m d`² – кинетическая энергия осевого движения атомов,
Е_rot(d) = М ² m^–1 d ^–2 – кинетическая энергия вращения молекулы вокруг оси, колинеарной вектору М суммарного момента импульса.
Введенная ранее величина μ₀ представляет собой значение энергии вращения при прохождении через минимум потенциальной энергии:
μ₀ = Е_rot(d₀)
Интеграл энергии I выражается через начальные значения:
I = ¼ m d`₀² + М ² m^–1 d₀ ^–2 + U(d₀).

• Энергия внутреннего движения I является интегралом движения и не зависит времени, тогда как все три её составляющие – кинетическая энергия осевого движения Е_ах, кинетическая энергия вращения молекулы Е_rot и потенциальная энергия U – являются переменными величинами, принимающими неотрицательные значения.

    Из (13) следует, что при заданных значениях интегралов движения Е и М энергия Е_ax является функцией одной обобщённой координаты – расстояния d между ядрами атомов:
       Е_аx = Е_аx(d),
где
       Е_аx(d) = I – Е_rot(d) – U(d).
При этом для всех значений расстояния d, возможных при заданных Е и М, должно выполняться неравенство:
       Е_аx(d) ≥ 0.                                                                                                      (14)
Можно сказать также, что при заданной величине d значения интегралов движения I и М не являются независимыми, а должны удовлетворять условию (14).

   Условия диссоциации молекулы и наличия режима колебаний

    Из определения функции Е_аx(d) следуют дифференциальные уравнения первого порядка относительно функции d(t):
          d` = 2 т<sup>– ½</sup> Е<sub>аx</sub>(d)<sup>½</sup>,                                                                                          (15)
если d`> 0 (ядра атомов отдаляются друг от друга);
          d` = – 2 т<sup>– ½</sup> Е<sub>аx</sub>(d)<sup>½</sup>,                                                                                       (16)
если d`< 0 (сближение ядер атомов)
Переключение между уравнениями (15) и (16) происходит в точках поворота траектории, т.е. в те моменты времени, когда d` = 0 или, иначе, когда расстояние d между ядрами атомов удовлетворяет уравнению
          Е_аx(d) = 0
или эквивалентному ему равенству
         I – Е_rot(d) = U(d).                                                                                                 (17)
Пусть М – произвольное значение момента импульса из интервала 0 ≤ М < М_С. Минимально возможное при данном М значение энергии I = I_min(М) соответствует чистому вращению с моментом импульса М, т.е. равновесному расстоянию d_eq(М) между атомами и отсутствию осевого движения:
I_min(М) = Е_rot(d_eq) + U(d_eq) = М ² m^–1 d_eq ^–2 + U(d_eq).
В частности, это означает, что выполняется равенство
         G(d_eq) = U(d_eq),
где
         G(d) = I_min(М) – Е_rot(d) = I_min(М) – М ² m^–1 d ^–2.
Иначе говоря, при чистом вращении равновесное расстояние d = d_eq(М) удовлетворяет уравнению (17). При этом, как нетрудно проверить, в силу условия равновесия (6) в точке d = d_eq(М) совпадают и производные функций G(d) и U(d), т.е. графики этих функций касаются, а уравнение (17) имеет двойной корень.

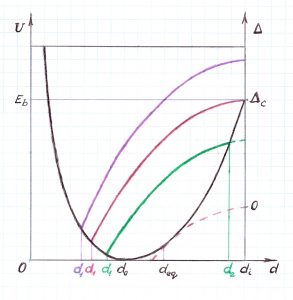
Рис. 2. Количество точек пересечений графиков U(d) и G(d) + Δ
для различных значений параметра Δ

      Смысл цветовых обозначений на Рис. 2
     Потенциал взаимодействия U(d): ─── 
     Графики функций G(d) + Δ при
                                            Δ > Δ_С:       ───
                                            Δ = Δ_С:       ───
                                            0 < Δ < Δ_С: ───
                                            Δ = 0:          ─  ─

    Если при том же значении М энергия I превышает энергию чистого вращения на величину Δ > 0, т.е.
       I = I_min(М) + Δ,
то, график функции
       I – Е_rot(d) = G(d) + Δ
сдвигается вверх на величину Δ по отношению к графику G(d), так что при достаточно малых Δ уравнение (17) имеет два различных корня d₁ и d₂, удовлетворяющих условию
        d₁ < d_eq(М) < d₂.
В этом случае расстояние между атомами колеблется в интервале d₁ ≤ d ≤ d₂ и одновременно происходит определяемое равенством (4) изменение угловой координаты каждого из них, т.е. атомы молекулы совершают свободные двумерные колебания, а величина Δ совпадает со значением энергии осевого движения в момент прохождения точки равновесия:
       Δ = Е_аx(d_eq).
С ростом Δ величина d₁ убывает, а d₂ – возрастает, пока не оказывается
       d₂ = d_i.                                                                                                            (18)
При дальнейшем увеличении Δ уравнение (17) имеет только один корень d₁, создающий поворот траектории при сближении атомов, а при их расхождении расстояние увеличивается неограниченно (движение атомов в молекуле инфинитно), т.е. молекула диссоциирует.
Предельному случаю (18) соответствуют критическое для данного М значение энергии I = I_С(М), определяемое формулой
       I_С(М) = Е_rot(d_i) + U(d_i) = М ² m^–1 d_i ^–2 + E_b,
и критическое значение добавки Δ = Δ_С(М), равное
       Δ_С(М) = I_С(М) – I_min(М).

• При заданной величине момента импульса М необходимым и достаточным условием существования молекулы является выполнение неравенств: 
                  М ≤ М_С,                                                                                                (19)
                 I ≤ I_С(М).                                                                                               (20)
  

   Свободные колебания

    Рассматривается случай, когда условия (19), (20) выполнены и, следовательно, атомы молекулы совершают свободные двумерные колебания.
Поскольку ветви траектории, соответствующие положительным и отрицательным значениям скорости изменения расстояния d`, полностью симметричны, можно исследовать только одну из них, описываемую дифференциальным уравнением (15). Как следует из (15), время t достижения расстояния d после прохождения нижнего амплитудного значения d₁ определяется формулой                                                                                                                                        d
      t = ½ т ^½ ∫ Е_аx(z)^{– ½} dz,                                                                (21)                                                                                                                                                                                                     d₁
а соответствующее выражение для периода колебаний Т имеет вид:                                                                                                                                                                                     d₂
    Т = т ^½ ∫ Е_аx(z)^{– ½} dz.                                                                          (22)                                                                                                                                                                                           d₁

• При выполнении условий финитности движения атомы двухатомной молекулы совершают свободные двумерные колебания с одновременным циклическим изменением расстояния между ядрами атомов и угловой скорости вращения. 
• В процессе колебаний меняются как кинетическая энергия осевого движения, так и кинетическая энергия вращения.

    Рассмотрим случай, когда амплитуда колебаний расстояния между ядрами атомов мала, так что в течение всего периода безразмерная переменная
       ξ = (d – d_eq) d_eq^–1
удовлетворяет условию
       |ξ| << 1.                                                                                                            (23)
При выполнении неравенства (23) кинетическая энергия вращения Е_rot(d) и потенциал взаимодействия U(d) могут быть в окрестности точки равновесия d_eq представлены в виде:
       Е_rot(d) = μ_eq (1+ ξ) ^–2 = μ_eq [1 – 2 ξ + 3 ξ² + О(ξ³)],                                           (24)
       U(d) = U(d_eq) – d_eq F(d_eq) ξ + α_eq ξ² + О(ξ³),                                                     (25)
где
       α_eq = ½  U »(d_eq) d_eq² – жёсткость связи в точке равновесия,
       μ_eq = Е_rot(d_eq) = М ² m^–1 d_eq^–2 – кинетическая энергия вращения в момент прохождения через точку равновесия.
С учётом уравнения равновесия (6) из (24), (25) следует разложение по степеням малого параметра ξ для функции Е_аx(d):
       Е_аx(d) = Δ – κ ξ² + О(ξ³),
где величина
       κ = α_eq + 3μ_eq                                                                                                  (26)
представляет собой эффективную жёсткость связи, учитывающую вращение.

• Эффективная жёсткость связи зависит от момента импульса М и не зависит от интеграла энергии Е.

     Таким образом, пренебрегая малыми величинами порядка О(ξ³), можно уравнение (17) относительно точек поворота траектории заменить квадратным уравнением
       κ ξ ² – Δ = 0,
корни которого имеют вид:
       ξ₁ = – а,
       ξ₂ = а,
где
       а = (Δ/κ) ^½.
В том же приближении формулы (21)-(22) представляются выражениями                                                                                                                                                                                          ξ
       t = ½ т ^½ d_eq ∫[Δ – κ ξ ²] ^{– ½} dξ =                                                               (27)                                                                                                                                                                                           ξ₁

     = ½ т ^½ d_eq κ ^{– ½} {π/2 + arcsin [(d/d_eq – 1) а ^{– 1}]},
       Т = π κ ^{– ½} т ^½ d_eq.
Обратная по отношению к (27) зависимость d = d(t) имеет при этом вид:
       d = d_eq – А cos ω t,
где
А = а d_eq = Δ ^½ κ ^–½ d_eq,                                                                                     (28)
ω = 2 κ^½  т ^–½ d_eq^–1.                                                                                          (29)

• Амплитуда малых колебаний А зависит как от момента импульса М, так и от энергии Е.
• Круговая частота малых колебаний ω зависит только от момента импульса.

     Зависимость частоты свободных колебаний от момента импульса  

    Поскольку равновесное расстояние d_eq зависит от момента импульса М, величины α_eq и μ_eq, а, значит, и κ также являются функциями от М. Как следует из (12), при выполнении условия (11) имеют место равенства:
       α_eq = (α₀ + α₁ ε)(1 + ε)² = α₀ + (2α₀ + α₁) ε + О(ε²),                                       (30)
       μ_eq = μ₀ (1 + ε) ^{– 2} = μ₀ + О(ε²),                                                                      (31)
где
       α₁ = ½  U »'(d₀) d₀³.
С учётом (30), (31) и определения (26) величины κ с точностью до малых порядка О(ε²) имеем:
       κ ≈ α₀ [1 + (5 + γ)ε],                                                                                       (32)
где
       γ = α₁/α₀ = U »'(d₀) d₀ / U »(d₀).

    Точное значение величины γ может быть найдено только в результате решения соответствующей задачи для уравнения Шрёдингера, однако некоторое представление о его величине можно получить с помощью известных аппроксимаций потенциала взаимодействия. В частности, популярная формула Леннарда-Джонса даёт результат:
       γ = – 21,
       5 + γ = – 16.
Как видно из (32), отрицательная величина выражения 5 + γ означает, что с ростом ε (т.е. с ростом момента импульса) эффективная жёсткость связи κ убывает, а, значит, растёт амплитуда колебаний А и убывает частота ω. Таким образом, есть основания полагать, что:

• с ростом момента импульса эффективная жёсткость связи  и частота малых свободных колебаний убывают, а амплитуда – растёт.

Дата последнего обновления:  2009-10-11